Estimating Muzzle Velocity via Gun Caliber

(Created September 2016)
(Revised April 2024)
IMPORTANT NOTE TO KEEP IN MIND ABOUT GUN CALIBERS:

The U.S. measured “calibre” as the length from the muzzle to the rear of the barrel (bore), while the Germans measured it from the muzzle to the rear of the breech. Thus, the US 90mm M3 gun would have a calibre of L50 under the US system and L52.5 under the German system.

Sometimes all you have on an artillery piece is the barest amount of data, particularly for German “Paper” guns in World War II, where they're described as “7.5cm KWK 42 L/100” and that's it.

However, there is a way to estimate muzzle velocity from gun caliber, due to a chance discovery.

A graph found in the November 1944 issue (#17) of Nachrichtenblatt der Panzertruppen (available on NARA RG 242 T78 Roll 623 and [HERE 18.8 MB PDF]) was reproduced and translated in Armoured Firepower: The Development of Tank Armament 1939-45 by Peter Gudgin.


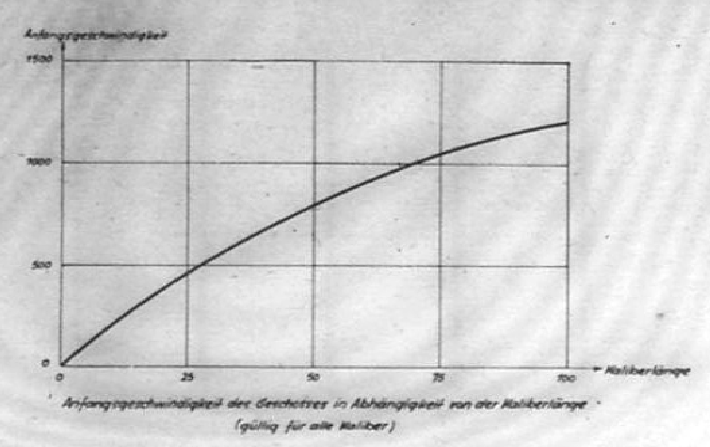
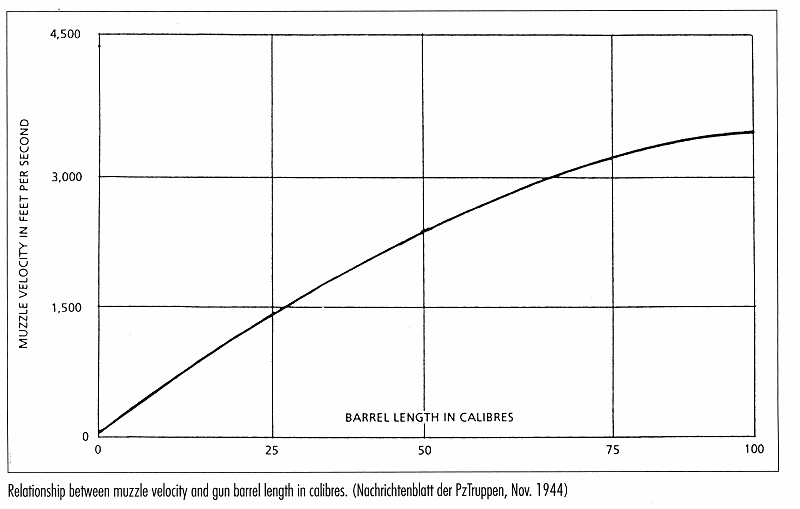
Original German Image from Nachrichtenblatt der Panzertruppen #17 (November 1944)


Translated version with Imperial units found in Armoured Firepower: The Development of Tank Armament 1939-45 by Peter Gudgin (Large Version)

What makes the Nachrichtenblatt der Panzertruppen graph so important is that it covers caliber ranges all the way down to L/0 and up to L/100, which are very hard to find easily accessible public data on, as guns in those ranges are experimental and aren't mentioned outside engineering or research reports.

After extracting the curve from the original German document via Engauge (RAW CSV File), I plotted as many guns as I could find, and found an extremely strong correlation, as shown below:


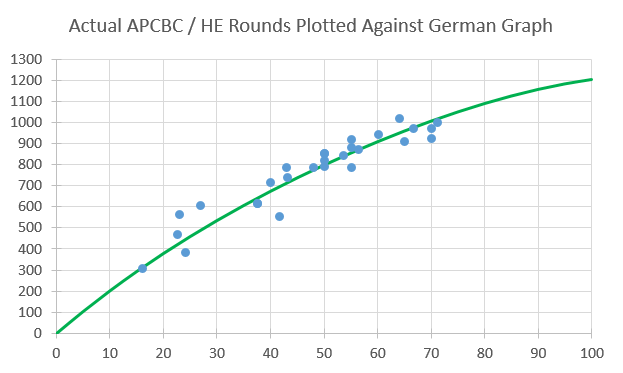
I then used Curve Expert's Linear Spline interpolator plus table generator to simplify the data down to THIS, which was in turn used to generate this 2nd Degree Polynominal Regression:

VM/Sec = [13.53596838 + (19.59394294 * C) + (-0.07734488 * C2)

Where C is Gun Caliber.

Calculator for Nachrichtenblatt der Panzertruppen Curve


Gun Caliber (L/x)

Muzzle Velocity (m/sec)

After analyzing the Nachrichtenblatt der Panzertruppen Caliber/Velocity Curve, I started to plot other types of ammunition and found that it fit pretty well with adjustments upwards for APCR (HVAP) rounds. Following this, I evaluated other rounds, resulting in the following curve(s) below:

Raw Data:

Caliber (L/x)

APBC/HE Curve (Baseline)

APCR Curve (Estimated)

APDS Curve (Estimated)

APDFS (Rifled) Curve (Estimated)

APDFS (Smoothbore) Curve (Estimated)

Curve % Adjustment
vs Baseline (L/50)

0

0

0

0

0

0

0.00%

5

105

129

154

180

210

13.14%

10

203

250

298

349

406

25.41%

15

294

363

433

506

589

36.80%

20

380

468

559

654

761

47.56%

25

460

567

677

792

922

57.57%

30

536

661

788

922

1,073

67.08%

35

607

749

893

1045

1,216

75.97%

40

675

832

992

1,161

1,351

84.48%

45

738

911

1,086

1,271

1,479

92.37%

50

799

985

1,175

1,375

1,600

100.00%

55

856

1,055

1,259

1,473

1,714

107.13%

60

910

1,122

1,338

1,566

1,822

113.89%

65

960

1,184

1,412

1,653

1,923

120.15%

70

1,007

1,242

1,482

1,734

2,018

126.03%

75

1,051

1,296

1,546

1,809

2,105

131.54%

80

1,091

1,345

1,605

1,878

2,185

136.55%

85

1,127

1,389

1,657

1,939

2,257

141.05%

90

1,158

1,428

1,703

1,993

2,319

144.93%

95

1,184

1,460

1,742

2,038

2,372

148.19%

100

1,205

1,486

1,772

2,074

2,413

150.81%

NOTES:

1.) Charts are based off using L50 entry as baseline and calculated using the percentage differences in the German AP/HE Curve to that L50 Baseline.

2.) When introducing APDS/APDFS Sabot Rounds, subtract about 100~ m/sec from the velocity to account for the newness of the type (APDS in WW2, APDFS rounds in the late 1950s/early 1960s)

3.) US Heavy Naval Guns generally have HE shells 60 to 100 m/sec faster than the AP shell for that gun. Use the APBC/HE curve as given for AP shells, and add 60-100 for HE shells.

USING THE DATA ABOVE

Let's say you have the 20 pounder gun, which is L/64, and you'd like to estimate the performance of a hypothetical “cut down” L/45 version for use in lightweight (compared to the Centurion) tanks circa 1946.

There may also be reasons to cut down the gun -- the most famous case is the US 76mm M1 Gun which was originally 57 calibers long in the prototypes, but cut down to 52 calibers for production versions to solve balance problems.

Example 1 (Directly from Chart):

This method is useful for completely hypothetical weapons that never actually existed.

Looking at the chart, you see that for a L/45 gun, performance would be about:

APCBC/HE: 740~ m/sec
APCR: 900~ m/sec
APDS: 986 to 1,000 m/sec (remember to subtract about 100 m/sec to take into account the fact that APDS shot was still in its infancy in 1946).

And if the tank somehow survives to the 1970s in active duty (a high probability in poorer countries), then you'd see 1,250~ m/sec APDFS rounds about then.

Example 2 (Adjustment of Actual Data):

For cases where you have actual shot data (20 pdr APDS was about 1,430 m/sec and caliber was L/64); you can adjust using the percentages:

L45 (92.37%)
L65 (120.15%)

0.9237 / 1.2015 = 0.7688

Adjusting the 1,430 m/sec shot (1,430 * 0.7688 = 1099.384) results in an APDS muzzle velocity of 1,100 m/sec.

If your caliber isn't in the table above, you can use the following 5th Degree Polynomial Regression to find the exact % of your gun caliber:

P = [0.0000413047822 + (0.02723449738 * C) + (-0.0001982993732 * C2) + (0.0000013589816 * C3) + (-0.0000000056517 * C4) + (-0.0000000000026 * C5)

Where C is Caliber and P is Percentage.

Calculator for Caliber %


Gun Caliber (L/x)

Caliber Percentage

Furthermore, you can estimate the future performance of your cut down gun if you take the L45 APDFS (Rifled) Curve (1271 m/sec) and divide it by the L45 APDS Curve (1086 m/sec).

This gives you a ratio of:

(1,271 / 1,086 = 1.1703)

This ratio can then be applied to your previously calculated 1,100 m/sec APDS velocity for a cut down L45 gun

1,100 * 1.1703 = 1,287.33 m/sec

Giving you a velocity of about 1,287 m/sec for the rifled fin stabilized sabot round of the 1970s for your cut down 20 pounder gun.